
« Gmane Size Analysis | Home | The Record Table »
The spelling table holds data used for suggesting spelling corrections. In the gmane database I'm analysing, it was generated after the database was, taking words from those indexed, but ignoring the rarer words. This means it contains fewer words than if every word in the database had been added. If all the words had been indexed for spelling correction, the n-gram tags would certainly be longer, and there would be more word frequency entries. There would probably be a few more n-gram entries too, which would have fairly short tags (since they wouldn't occur in many words).
Table size: 1,287,199 entries in 9,410 8KB blocks (73.5MB).
| Level | Number of blocks | Comment |
|---|---|---|
| 2 | 1 | The root block |
| 1 | 19 | |
| 0 | 9,390 | Leaf blocks, which hold the tag data |
Key size range: 3 to 65 bytes (mean 10.29).
Frequency range: 6 to 136,391 occurrences of a particular key size.
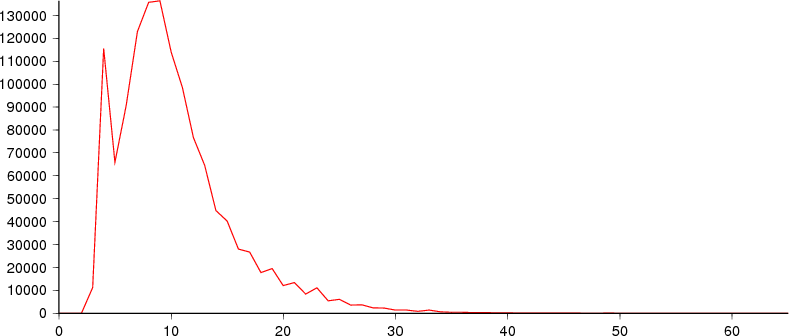
The spelling table contains two distinct types of entries - frequencies of words, and mappings from bigrams and trigrams to lists of words. For details of the format, the description of the format for Flint on the wiki is also valid for Chert.
The initial spike in keysize is largely due to the 4 byte keys from trigrams. There will also be a number of 3 byte keys from bigrams, but far fewer as there aren't nearly as many possible bigrams.
The larger, wider peak is from the keys for word frequency entries.
The majority of keys are pretty short, so adding prefix compression of keys won't make a huge difference here.
The first byte of a key is one of 5 values ('B', 'H', 'M', 'T', 'W'). We could shave a byte off the majority of these keys with a slightly more complex key encoding scheme. That's probably not worthwhile if we're going to prefix compress keys anyway though.
Tag size range: 1 to 167,171 bytes (mean 40.12).
Frequency range: 1 to 618,569 occurrences of a particular tag size.
Total size of all tags is 49.2MB.

It's hard to see from the above plot, but there's a large spike close to the Y-axis, and a fairly flat distribution along the X axis. The large spike will be largely due to the word frequency entries (which will have a tag size of 1-4 bytes) and the rest will be due to the lists of words matching a particular bigram or trigram.
This plot has log(1 + frequency) on the Y axis and shows the distribution more clearly:
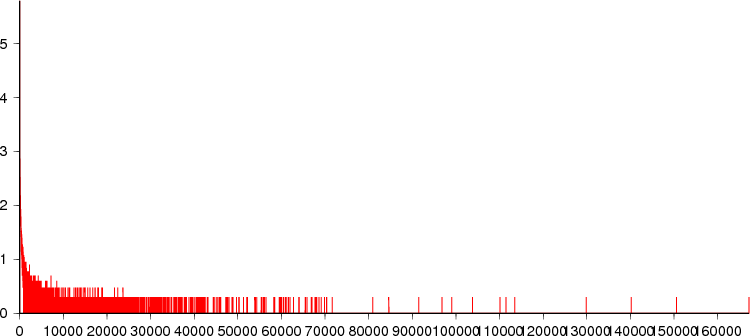
There are some very large tags, but most are a more modest size. The splitting of tags when the key + tag + overhead is more than 1/4 of the block size will mean we split quite a lot of tags here - there are 23,202 continuation items for the 1,287,199 entries.
| Item | Total size (bytes) | Per entry (bytes) | Per leaf block (bytes) |
|---|---|---|---|
| Per entry overhead | 11,584,791 | 9.0000 | 1,233.7371 |
| Overhead in leaf blocks from split tags | 297,695 | 0.2313 | 31.7034 |
| 20 branch blocks | 163,840 | 0.1273 | 17.4483 |
| Leaf block headers | 103,290 | 0.0802 | 11.0000 |
| Unused space in leaf blocks | 53,313 | 0.0414 | 5.6776 |
Note that the per entry overhead dominates - the other overheads add up to less than a byte per entry, so shaving a single byte off the per entry overhead will make more difference than can be got from completely eliminating all the other overheads.
This is the smallest table in the gmane database by a long way, and it is likely to be one of the smallest tables for any database. So improvements here aren't likely to save as much space as improvements to the other tables.
Prefix compressing keys and reducing the per entry overhead are likely to make the most difference here.
While it wouldn't save much space, it might be interesting to look at the small number of really large tags to see if they could be stored more compactly, as they may currently result in slow cases for spelling correction.
Posted in xapian by Olly Betts on 2009-12-14 17:07 | Permalink